relliptical R
packageThe relliptical R package offers random numbers
generation from members of the truncated multivariate elliptical family
of distribution such as the truncated versions of the Normal, Student-t,
Laplace, Pearson VII, Slash, Logistic, Kotz-type, among others.
Particular distributions can be provided by specifying the density
generating function. It also computes the first two moments (covariance
matrix as well) for some particular distributions. For more details see
(Valeriano, Galarza, and Matos 2023).
Next, we will show the functions available in the package.
The function rtelliptical generates observations from a
truncated multivariate elliptical distribution with location parameter
mu, scale matrix Sigma, lower and upper
truncation points lower and upper via Slice
Sampling algorithm (Neal 2003) with Gibbs sampler (Robert and Casella
2010) steps. The dist argument represents the truncated
distribution to be used. The values are Normal,
t, Laplace, PE,
PVII, Slash, and CN, for the
truncated Normal, Student-t, Laplace, Power Exponential, Pearson VII,
Slash, and Contaminated Normal distributions, respectively.
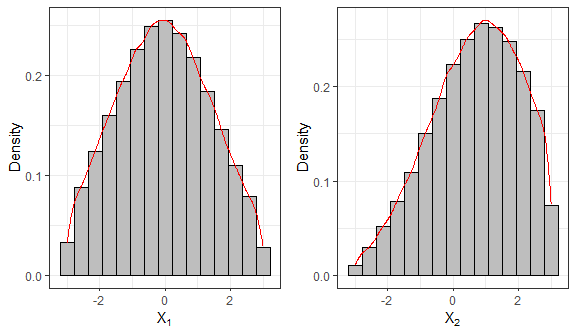
In the following example, we generate \(n = 10^5\) samples from the truncated bivariate Normal distribution.
library(relliptical)
# Sampling from the Truncated Normal distribution
set.seed(1234)
mu = c(0, 1)
Sigma = matrix(c(3,0.6,0.6,3), 2, 2)
lower = c(-3, -3)
upper = c(3, 3)
sample1 = rtelliptical(n=1e5, mu, Sigma, lower, upper, dist="Normal")
head(sample1)
#> [,1] [,2]
#> [1,] 0.6643105 2.4005763
#> [2,] -1.3364441 -0.1756624
#> [3,] -0.1814043 1.7013605
#> [4,] -0.6841829 2.4750461
#> [5,] 2.0984490 0.1375868
#> [6,] -1.8796633 -1.2629126
library(ggplot2)
# Histogram and density for variable 1
f1 = ggplot(data.frame(sample1), aes(x=X1)) +
geom_histogram(aes(y=after_stat(density)), colour="black", fill="grey", bins=15) +
geom_density(colour="red") + labs(x=bquote(X[1]), y="Density") + theme_bw()
# Histogram and density for variable 2
f2 = ggplot(data.frame(sample1), aes(x=X2)) +
geom_histogram(aes(y=after_stat(density)), colour="black", fill="grey", bins=15) +
geom_density(colour="red") + labs(x=bquote(X[2]), y="Density") + theme_bw()
library(gridExtra)
grid.arrange(f1, f2, nrow=1)
This function also allows generating random numbers from other
truncated elliptical distributions not specified in the
dist argument, by supplying the density generating function
(DGF) through arguments either expr or gFun.
The DGF must be a non-negative and strictly decreasing function on \((0, \infty)\). The easiest way is to
provide the DGF expression to argument expr as a character.
The notation used in expr needs to be understood by package
Ryacas0 and the environment of R. For
instance, for the DGF \(g(t)=e^{-t}\),
the user must provide expr = "exp(1)^(-t)". See that the
function must depend only on variable \(t\), and any additional parameter must be
passed as a fixed value. For this case, when a character expression is
provided to expr, the algorithm tries to compute a
closed-form expression for the inverse function of \(g(t)\), however, this is not always
possible (a warning message is returned).
The following example draws random variates from a truncated bivariate Logistic distribution, whose DGF is given by \(g(t) = e^{-t}/(1+e^{-t})^2, t \geq 0\), see (Fang, Kotz, and Ng 2018).
# Sampling from the Truncated Logistic distribution
mu = c(0, 0)
Sigma = matrix(c(1,0.70,0.70,1), 2, 2)
lower = c(-2, -2)
upper = c(3, 2)
# Sample autocorrelation with no thinning
set.seed(5678)
sample2 = rtelliptical(n=1e4, mu, Sigma, lower, upper, expr="exp(1)^(-t)/(1+exp(1)^(-t))^2")
tail(sample2)
#> [,1] [,2]
#> [9995,] -0.5639346 -1.4225548
#> [9996,] -0.4747796 -1.1890135
#> [9997,] -0.2596561 -0.1126482
#> [9998,] -1.1517285 -0.9875129
#> [9999,] -0.9268744 -1.5526844
#> [10000,] -1.1763390 -1.3098489If it was no possible to generate random samples by passing a
character expression to expr, the user may provide a custom
R function to the gFun argument. By default,
its inverse function is approximated numerically, however, the user may
also provide its inverse to the ginvFun argument to gain
some computational time. When gFun is provided, arguments
dist and expr are ignored.
In the next example, we will draw samples from the truncated Kotz-type distribution, whose DGF is given by
\[g(t) = t^{N-1} e^{-r t^s}, \quad t\geq 0, \quad r>0, \quad s>0, \quad 2N+p>2.\]
As required, this function is strictly decreasing when \((2-p)/2 < N \leq 1\), see (Fang, Kotz, and Ng 2018).
# Sampling from the Truncated Kotz-type distribution
set.seed(9876)
mu = c(0, 0)
Sigma = matrix(c(1,0.70,0.70,1), 2, 2)
lower = c(-2, -2)
upper = c(3, 2)
sample4 = rtelliptical(n=1e4, mu, Sigma, lower, upper, gFun=function(t){ t^(-1/2)*exp(-2*t^(1/4)) })
f1 = ggplot(data.frame(sample4), aes(x=X1, y=X2)) + geom_point(size=0.50) +
labs(x=expression(X[1]), y=expression(X[2]), subtitle="Kotz(2,1/4,1/2)") + theme_bw()
library(ggExtra)
ggMarginal(f1, type="histogram", fill="grey")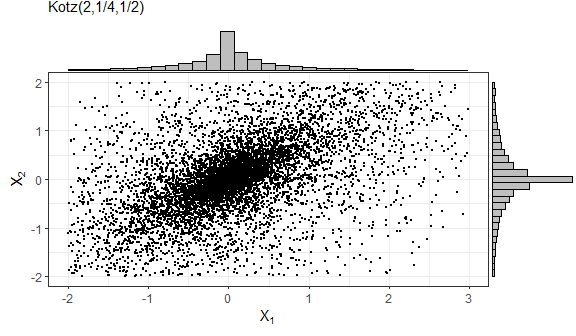
Since the generating process uses an MCMC method, observations will be correlated, so it may be of interest to study some ACF plots. Now, we study the sample from the bivariate logistic distribution.
grid.arrange(grobs=acf.plot(sample2), top="Sample ACF with no thinning", nrow=1)
Autocorrelation can be decimated by setting the thinning
argument. The thinning factor reduces the autocorrelation of the random
points in the Gibbs sampling process. Thinning consists in picking
separated points from the sample, at each k-th step. As natural, this
value must be an integer greater than or equal to 1.
# Sample autocorrelation with thinning = 3
set.seed(8768)
sample3 = rtelliptical(n=1e4, mu, Sigma, lower, upper, dist=NULL, expr="exp(1)^(-t)/(1+exp(1)^(-t))^2",
thinning=3)
grid.arrange(grobs=acf.plot(sample3), top="Sample ACF with thinning = 3", nrow=1)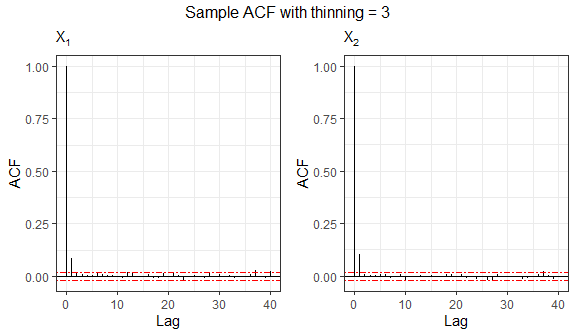
For this purpose, we call the function mvtelliptical(),
which returns the mean vector and variance-covariance matrix for some
specific truncated elliptical distributions. The argument
dist sets the distribution to be used and accepts the same
values Normal, t, Laplace,
PE, PVII, Slash, and
CN as before. Moments are computed through Monte Carlo
method for the truncated variables and using properties of the
conditional expectation for the non-truncated variables.
Next, we compute the moments for a random variable \(X\) following a truncated 3-variate Student-t distribution with \(\nu=0.8\) degrees of freedom. We will consider two scenarios: a first one with only one doubly truncated variable, and a second one with two doubly truncated variables.
# Truncated Student-t distribution
set.seed(5678)
mu = c(0.1, 0.2, 0.3)
Sigma = matrix(data = c(1,0.2,0.3,0.2,1,0.4,0.3,0.4,1), nrow=length(mu), ncol=length(mu), byrow=TRUE)
# Example 1: one doubly truncated student-t (nu = 0.80)
a = c(-0.8, -Inf, -Inf)
b = c(0.5, 0.6, Inf)
mvtelliptical(a, b, mu, Sigma, "t", 0.80)
#> $EY
#> [,1]
#> [1,] -0.11001805
#> [2,] -0.54278399
#> [3,] -0.01119847
#>
#> $EYY
#> [,1] [,2] [,3]
#> [1,] 0.13761136 0.09694152 0.04317817
#> [2,] 0.09694152 NaN NaN
#> [3,] 0.04317817 NaN NaN
#>
#> $VarY
#> [,1] [,2] [,3]
#> [1,] 0.12550739 0.03722548 0.04194614
#> [2,] 0.03722548 NaN NaN
#> [3,] 0.04194614 NaN NaN
# Example 2: considering nu = 0.80 and two doubly truncated variables
a = c(-0.8, -0.70, -Inf)
b = c(0.5, 0.6, Inf)
mvtelliptical(a, b, mu, Sigma, "t", 0.80) # By default n=1e4
#> $EY
#> [,1]
#> [1,] -0.08566441
#> [2,] 0.01563586
#> [3,] 0.19215627
#>
#> $EYY
#> [,1] [,2] [,3]
#> [1,] 0.126040187 0.005937196 0.01331868
#> [2,] 0.005937196 0.119761635 0.04700108
#> [3,] 0.013318682 0.047001083 1.14714388
#>
#> $VarY
#> [,1] [,2] [,3]
#> [1,] 0.118701796 0.007276632 0.02977964
#> [2,] 0.007276632 0.119517155 0.04399655
#> [3,] 0.029779636 0.043996554 1.11021985As seen for the first scenario, some elements of the
variance-covariance matrix are shown as NaN. Those are the
cases where the moment does not exist (yes, some elements of the
variance-covariance matrix may exist and others may not). It is well
know that for a Student-t distribution its second moment exist if \(\nu>2\), however, as studied by (Galarza
et al. 2022), this condition is relaxed as the number of dimensions
containing only finite truncation limits increases.
It is worth mention that the Student-\(t\) distribution with \(\nu > 0\) degrees of freedom is a particular case of the Pearson VII distribution with parameters \(m > p/2\) and \(\nu^* > 0\) when \(m = (\nu+p)/2\) and \(\nu^* = \nu\).
Finally, for comparison purposes, we compute the moments for a doubly truncated Pearson VII distribution with parameters \(\nu^* = \nu = 0.80\) and \(m = (\nu + 3)/2 = 1.90\), which is equivalent to the Student-t distribution mentioned above. Therefore, their moments should be nearly equal.
# Truncated Pearson VII distribution
set.seed(9876)
a = c(-0.8, -0.70, -Inf)
b = c(0.5, 0.6, Inf)
mu = c(0.1, 0.2, 0.3)
Sigma = matrix(data = c(1,0.2,0.3,0.2,1,0.4,0.3,0.4,1), nrow=length(mu), ncol=length(mu), byrow=TRUE)
mvtelliptical(a, b, mu, Sigma, "PVII", c(1.90,0.80), n=1e6) # n=1e6 more precision
#> $EY
#> [,1]
#> [1,] -0.08558130
#> [2,] 0.01420611
#> [3,] 0.19166895
#>
#> $EYY
#> [,1] [,2] [,3]
#> [1,] 0.128348258 0.006903655 0.01420704
#> [2,] 0.006903655 0.121364742 0.04749544
#> [3,] 0.014207043 0.047495444 1.15156461
#>
#> $VarY
#> [,1] [,2] [,3]
#> [1,] 0.121024099 0.008119433 0.03061032
#> [2,] 0.008119433 0.121162929 0.04477257
#> [3,] 0.030610322 0.044772574 1.11482763